12-watt devices like LED bulbs draw a small amount of current. That allows multiple pieces to be connected in a single circuit. If we would like to put multiple LED bulbs in one branch circuit, we have to know how many amps is 12 watts.
12 watts may be 1 amp at 12V DC, 0.10 amps at 120V single phase AC, 0.05 amps at 240V single phase AC, and 0.03 amps at 208V three phase.
Want to learn how we come up with these numbers? Read on to find out!
Table of Contents
The Relation Between Amps and Watts
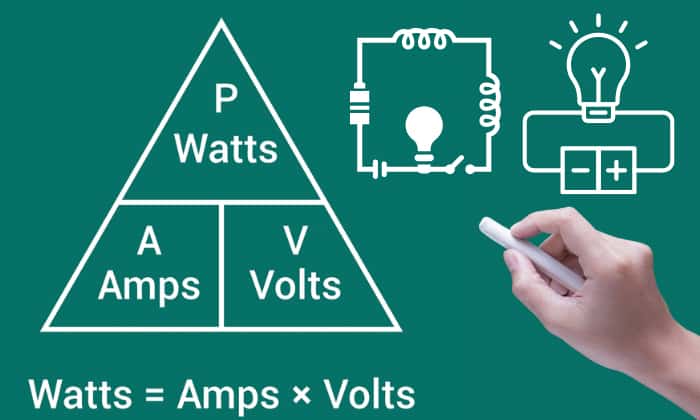
Power is the rate of energy used per second, and is defined by voltage and current for electric power:
\[ \text{Electric Power (in watt)} = \frac{\text{Energy (in joule)}}{\text{Time (in second)}} = \text{Current (in ampere)} \times \text{Voltage (in volt)} \]
We can derive the basic amperes calculation formula from this relationship:
\[ \text{Current (in ampere)} = \frac{\text{Power (in watt)}}{\text{Voltage (in volt)}} \]
The formula shows that an appliance will draw lower currents at higher voltages at a constant 12 W. It also shows us that the unit amp = watts/volts.
Moreover, you can utilize the tool for a rapid assessment of amperage.
How to Solve Amps From Watts?
Here’s how you can use watts to find the value of amps in direct and alternating currents.
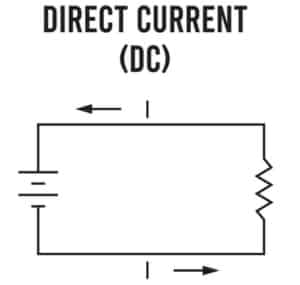
1. Direct current (DC)
DC, or direct current supply has a constant current to the voltage terminals in a closed circuit. To find amps from watts in a DC supply, we can simply use the amperes calculation formula earlier.
Let’s try it on 12 watts. Let’s find the amp draw of a 12-watt LED bulb from a 12-volt lead acid battery. The current drawn by the load is:
\[ \text{Current} = \frac{\text{Power}}{\text{Voltage}} = \frac{12 \, \text{watts}}{12 \, \text{volts}} = 1 \, \text{amp} \]
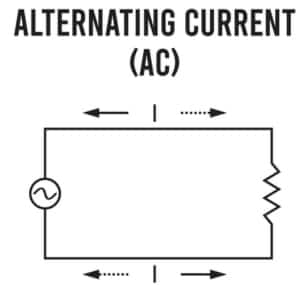
2. Alternating current (AC), single phase
alternating current, or AC, has varying voltages and thus, varying current. The electrical supply has a frequency of 60 Hz, and the residential supply is commonly a 240-volt line-to-line single phase with a 120-volt line-to-neutral connection.
Sometimes, power factors have to be introduced for AC supply. Power factors correct power losses when varying voltage does not match the varying current cycles and are expressed as
\[ \text{Power Factor} = \frac{\text{Actual power (in watt)}}{\text{Apparent power (in volt $\times$ ampere)}} \]
where the output is the actual power and the input is the apparent power. They range from 0 to 1, with 1 indicating no power loss.
When we compute the current that appliances draw in AC, we consider its power factor. The equation that we will use is slightly different from our previous converter equation in DC:
\[ \text{Current (in ampere)} = \frac{\text{Actual power (in watt)}}{\text{Power Factor} \times \text{voltage (in volt)}} \]
Let’s compute for the amp draw of our 12 watt LED bulb at 220V. If the light bulb’s power factor is 0.95, then:
\[ \text{Current} = \frac{\text{Actual power}}{\text{Power Factor} \times \text{voltage}} \]
\[ f = \frac{12 \, \text{W}}{0.95 \times 220 \, \text{V}} = 0.057 \, \text{A} \quad \text{or} \quad 57 \, \text{mA} \]
*Note: Lighting in the US is normally connected to the 120-volt supply. The calculation above is just an example.
3. Alternating current (AC), three phase
Three-phase current is more common in commercial establishments. Three-phase current is like 3 single-phase supplies combined together with 120 degrees phase difference. Commercial supply commonly has a line-to-line supply at 208 volts and a line-to-neutral supply at 120 volts.
The line-to-neutral supply is just a single-phase 120-volt AC supply. We can use the same equation to solve amps from watts:
\[ \text{Current (in ampere)} = \frac{\text{Actual power (in watt)}}{\text{Power Factor} \times \text{voltage (in volt)}} \]
The line-to-line supply needs to consider the phase difference associated with three-phase supply. The current draw in the line-to-line supply may be estimated using:
\[ \text{Current (in ampere)} = \frac{\text{Actual power (in watt)}}{\sqrt{3} \times \text{Power Factor} \times \text{voltage}_{\text{L-L}} \, \text{(in volt)}} \]
For example, if we connect 12 watt LED bulb with 0.95 power factor at line-to-line, then the current draw will be
\[ \text{Current (in ampere)} = \frac{\text{Actual power (in watt)}}{\sqrt{3} \times \text{Power Factor} \times \text{voltage}_{\text{L-L}} \, \text{(in volt)}} \]
\[= \frac{12 \, \text{W}}{\sqrt{3} \times 0.95 \times 208 \, \text{V}} = 0.035 \, \text{A} \quad \text{or} \quad 35 \, \text{mA} \]
*Note: Lighting in the US is normally connected to the 120-volt supply. The calculation above is just an example.
Watts Conversion to Amps
We made a simple conversion table at common voltages. We’ve listed the current draws of 12 watts and close values for DC supply and AC supply in single phase and three phase at different power factors:
| Power | Current | ||||||||||
| DC | AC | ||||||||||
| Line-to-Neutral for Single and Three phase | Single Phase Line-to-Line | Three Phase Line-to-Line | |||||||||
| 12V | 24V | 120V | 240V | 208V | |||||||
| – | – | PF at 1 | PF at 0.85 | PF at 0.5 | PF at 1 | PF at 0.85 | PF at 0.5 | PF at 1 | PF at 0.85 | PF at 0.5 | |
| 10W | 0.83A | 0.42A | 0.08A | 0.10A | 0.17A | 0.04A | 0.05A | 0.08A | 0.03A | 0.03A | 0.06A |
| 10.5W | 0.88A | 0.44A | 0.09A | 0.10A | 0.18A | 0.04A | 0.05A | 0.09A | 0.03A | 0.03A | 0.06A |
| 11W | 0.92A | 0.46A | 0.09A | 0.11A | 0.18A | 0.05A | 0.05A | 0.09A | 0.03A | 0.04A | 0.06A |
| 11.5W | 0.96A | 0.48A | 0.10A | 0.11A | 0.19A | 0.05A | 0.06A | 0.10A | 0.03A | 0.04A | 0.06A |
| 12W | 1.00A | 0.50A | 0.10A | 0.12A | 0.20A | 0.05A | 0.06A | 0.10A | 0.03A | 0.04A | 0.07A |
| 12.5W | 1.04A | 0.52A | 0.10A | 0.12A | 0.21A | 0.05A | 0.06A | 0.10A | 0.03A | 0.04A | 0.07A |
| 13W | 1.08A | 0.54A | 0.11A | 0.13A | 0.22A | 0.05A | 0.06A | 0.11A | 0.04A | 0.04A | 0.07A |
| 13.5W | 1.13A | 0.56A | 0.11A | 0.13A | 0.23A | 0.06A | 0.07A | 0.11A | 0.04A | 0.04A | 0.07A |
| 14W | 1.17A | 0.58A | 0.12A | 0.14A | 0.23A | 0.06A | 0.07A | 0.12A | 0.04A | 0.05A | 0.08A |
The table includes calculations for power factors at 1, 0.85, and 0.5. You can also use volts, amps, and watts calculator available online for specific conditions that you need that are not found in this table.
The Impact of AC and DC on Power Conversion
The key difference between AC and DC circuits in terms of power conversion lies in how the voltage and current vary.
In an AC circuit, the voltage and current periodically change direction and magnitude. The current alternates back and forth, reversing its direction periodically, while the voltage follows a similar pattern.
In a DC circuit, the voltage remains constant, and the current flows consistently in one direction without changing polarity.
Since the DC supply does not cycle, it does not have the power loss that power factors correct (remember that power factors correct power losses that happen when cycling voltage is out of phase with cycling current).
Why We Should Calculate Amperage of Appliances
12 watts seems like a small value. However, calculating the amperage helps to determine the maximum number of 12-watt appliances you can place in a branch circuit before overloading occurs.
For example, let’s say you want to use a cheap 12-watt light bulb with a power factor of 0.5 for an entire building and place them in a 15-amp circuit (with a 12-amp limit for continuous loads). Based on our table, the current draw will be 0.20 amps. You can fit 60 bulbs in that circuit before the circuit overloads.
Conclusion
If we want to know how many amps is 12 watts, then we can use the equations for DC or AC supply in single-phase or three-phase to solve amps from watts at various voltages. The current may range from 0.1 amp to 1 amp depending on the voltage and the type of supply.
The calculation for each supply may be different from each other, but calculating amps from watts can help prevent circuit overloading. It can also be used to properly estimate the number of loads that can safely be placed in the circuit.
Read more: Convert 50 watts, 40 watts to amps.

I am Edwin Jones, in charge of designing content for Galvinpower. I aspire to use my experiences in marketing to create reliable and necessary information to help our readers. It has been fun to work with Andrew and apply his incredible knowledge to our content.